COVID-19 outbreak

IBM Ponder This is a monthly puzzle. Most people find the puzzles fairly difficult to solve. Solutions typically require a combination of software engineering (encoding the problem as a search) and math (or some other form of insight) to reduce the search space. Simple bruteforce usually doesn’t lead anywhere.

Each previous month’s solution is made available. However, solutions are typically very succinct and don’t explain how the solution was obtained. The purpose of this write up is to expose my thought process (and wrong turns) which eventually lead me to solve April 2020’s challenge. Companion code, written in Go, is available at github.com/alokmenghrajani/ponderthis-april2020

Puzzle

This month's challenge is inspired by the COVID-19 pandemic.

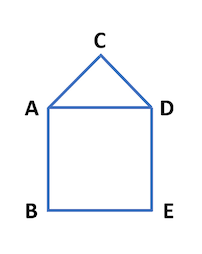
Suppose that the world has five cities and they are all connected to one another as depicted by the five-verticed graph in the following picture:

Let's assume that the infection passes daily along the edges. So, if on day t, "D" is infected and "C" is healthy, then "C" has a 10% chance of getting infected, by "D", on day t+1. If "A" is infected at time 0, after ten days, there is about a 29.16521896% probability that all five will be infected.

Find a graph with no more than eight vertices that gives a probability of 70.00% (accurate to the second decimal digit after the decimal point) of all cities/vertices being infected after ten days.

Give your answer as an adjacency matrix.
For example, the adjacency matrix of the graph depicted above is

01110
10001
10010
10101
01010

Bonus '*' for getting the closest to 70% in 19 days; and ’**' for getting even closer. Current best is less than 1.9E-7 away from 0.7.

We were seeking the answer of Day 19 (which can give a solution with a better approximation), but we also accepted answers for Day 10.

Part 1: computing probability after N days

The first step is to implement code which computes the probability for a given graph to have all its vertices infected after N days. We have a sample input and answer, so we’ll know if our first step is maybe correct or definitely wrong.

Recursive function to compute exact value

The simplest way to compute the exact value is to use a recursive function f(days, graph, state), where days represents the number of days left and state tracks which vertices in graph are infected. We define f as following:

1. f(..., graph, state) is 1.0 if all the vertices are infected
2. f(0, ..., ...) is 0.0. The base case.
3. f(N, graph, state) is equal to r:
   • Starting with r = 0.0
   • For every combination of edge with exactly one infected vertex,
     r += 10% * f(N-1, graph, state with both vertices infected) + 90% * f(N-1, graph, unchanged state)

The following commands will show you part 1 in action. We can confirm that we get the expected value for the sample:

$ git clone https://github.com/alokmenghrajani/ponderthis-april2020.git

$ go build

$ ./ponderthis-april2020 compute --algorithm recursive --graph 01110,10001,10010,10101,01010 --days 10
probability of all vertices infected after 10 days: 29.16521896015063%

The source code lets you peek at the exact details. Computing every combination of edges requires its own recursive function and combining probabilities.

At this point, we don’t know whether or not our code is correct. One way to build some confidence is to implement a few test cases which are easy to reason about. E.g. increasing the number of days should make the result go towards 100%:

$ ./ponderthis-april2020 compute --algorithm recursive --graph 01110,10001,10010,10101,01010 --days 20
probability of all vertices infected after 20 days: 79.42213869586355%

$ ./ponderthis-april2020 compute --algorithm recursive --graph 01110,10001,10010,10101,01010 --days 30
probability of all vertices infected after 30 days: 96.00377231566937%

$ ./ponderthis-april2020 compute --algorithm recursive --graph 01110,10001,10010,10101,01010 --days 40
probability of all vertices infected after 40 days: 99.3438646251387%

Unless the graph is disconnected, in which case the value should remain 0%:

$ ./ponderthis-april2020 compute --algorithm recursive --graph 0100,1000,0001,0010 --days 10
probability of all vertices infected after 10 days: 0%

We can also compare the result of a dense connected graph vs a sparse connected one. We expect dense graphs to converge quicker towards 100% (an intuition which is going to be useful later).

vs

$ ./ponderthis-april2020 compute --algorithm recursive --graph 01110,10001,10010,10100,01000 --days=10
probability of all vertices infected after 10 days: 16.051861857290785%

$ ./ponderthis-april2020 compute --algorithm recursive --graph 01110,10111,11010,11101,01010 --days=10
probability of all vertices infected after 10 days: 43.363910981826784%

Part 2: graph enumeration

Once we can compute a given graph’s probability to have all infected vertices after N days, we need to search for a graph. A naive approach would be to search over all possible adjacency matrices. Assuming our graphs are undirected, there are 2^28 matrices with 8 vertices. This is not a very large number (~270M) as long as our computation function is fast.

Searching for all possible matrices is wasteful: isomorphic graphs (graphs which are identical except for the ordering of the vertices) would yield identical results (ignoring the fact that the first vertex is special since it’s where the infection starts). Telling if two graphs are isomorphic is NP hard (i.e. computationally expensive). We have two options:

1. Enumerate graphs in a way which gives us only one instance of each isomorphism class. To achieve this, you need a bit of math background — a good starting point is Brendan McKay and Adolfo Piperno’s Nauty & Traces project.
2. Download a database of graphs from Brendan McKay’s website.

I downloaded the database of graphs, which reduces the search space to 12,112 graphs (all connected simple graphs with 2-8 vertices). For any given graph, we must however consider any of the vertices as the initially infected vertex, which gives us a total search space of 95,716 (about 3000x more efficient than trying every possible adjacency matrix).

Solving takes a few hours but we eventually get a solution with 7 vertices:

$ ./ponderthis-april2020 solve --graphs graphs.txt --algorithm=recursive --days=19
…
Improved solution! v=0.6999523879097757
0011010
0000111
1000011
1000011
0100001
1111001
0111110
…

Part 3: achieving the bonus ‘*’

If we want to get a better solution, we need our computation to happen quicker. There are a few ways to optimize things: rewrite the code to leverage all the cores (the code is “single threaded”), write the code to run on a GPU, sort the graphs based on number of edges and prioritize those more likely to yield a solution (we know that the solution can’t have too few or too many edges), use a simulation to get an approximate value to filter graphs and only compute exact values in a subset of cases, etc.

Two simpler ways to speed things up are to implement memoization or use dynamic programming techniques. I decided to go the dynamic programming way, which is just a fancy way of saying: instead of recursing top-down, build a table of all possible states for each day and replace the recursion with a table lookup. This is a typical cpu-memory tradeoff; a tradeoff software engineers have to often consider. Building the table is done iteratively, starting from the case where there’s 0 days left.

Using a faster function to process each graph, we quickly find the best solution for 19 days (this code is about 1,000,000x faster!):

$ ./ponderthis-april2020 solve --graphs graphs.txt --algorithm=dp --days=19
…
best: 0.7000008653156911, eta: 0s
best solution
01110001
10001000
10000110
10000011
01000011
00100001
00111000
10011100

Part 4: double bonus ‘**’

Searching for the best result over any number of days, every graph has an upper bound of days where it crosses our target probability. With some minor changes, computing subsequent days for each graph yields the answer:

…
best: 0.6999998106703065, days: 28, eta: 0s
best solution
0100000
1000111
0000111
0000011
0110001
0111000
0111100

Final words

Hope you enjoyed this write up and accompanying source code. I left out some of the rabbit holes I stumbled across, such as Markov Models and digraphs (the ‘**’ bonus wasn’t very clear to me). Ponder This challenges can sometimes be solved by finding a clever way to divide and conquer the problem into smaller chunks — my attempt to find such a subdivision was unsuccessful.

Following is a short collection of writeups by various other people for other IBM Ponder This challenges:

• July 2018 (Aging Obscure Triplets) by srcmake
• January 2019 (Charlie helps Bob defeat Alice) by Gdasl
• February 2019 (Debater's score) by Gdasl
• April 2019 (Prime magic square) by Marcelo M De Barros
• May 2019 (Longest boat trip) by Thomas Huet
• r/ponderthis has a few solutions from 2015-2016.